Data Displays & Analysis6th Grade |
|
|---|---|
Alabama Course of Study Standards: 22 |
|
Write examples and non-examples of statistical questions, explaining that a statistical question anticipates variability in the data related to the question |
|
Arizona Academic Standards: 6.SP.A.1 |
|
Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for variability in the answers. For example, "How old am I?" is not a statistical question, but "How old are the students in my school?" is a statistical question because one anticipates variability in students' ages. |
|
Common Core State Standards: Math.6.SP.1 or 6.SP.A.1Florida - Benchmarks for Excellent Student Thinking: MAFS.6.SP.1.1 |
|
Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers. For example, “How old am I?” is not a statistical question, but “How old are the students in my school?” is a statistical question because one anticipates variability in students’ ages. |
|
North Carolina - Standard Course of Study: 6.SP.1 |
|
Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers. |
|
New York State Next Generation Learning Standards: 6.SP.1 |
|
e.g., "How old am I?" is not a statistical question, but "How old are the students in my school?" is a statistical question because one anticipates variability in students' ages. Note: Students need to understand that data are generated with respect to particular contexts or situations and can be used to answer questions about those contexts or situations. Note: Examples of acceptable methods to obtain a representative sample from a population include, but are not limited to, a simple random sample for a given population or a systematic random sample for an unknown population. Examples of unacceptable methods of sampling include, but are not limited to, online polls and convenience sampling because they introduce bias and are not representative of the population. |
|
Ohio's Learning Standards: 6.SP.1 |
|
Develop statistical reasoning by using the GAISE model: |
|
Tennessee Academic Standards: 6.SP.A.1 |
|
Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers. For example, "How old am I?" is not a statistical question, but "How old are the students in my school?" is a statistical question because one anticipates variability in students' ages. |
|
Wisconsin Academic Standards: 6.SP.A.1 |
|
Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers. |
|
Arizona Academic Standards: 6.SP.A.2 |
|
Understand that a set of data collected to answer a statistical question has a distribution whose general characteristics can be described by its center, spread, and overall shape. |
|
Common Core State Standards: Math.6.SP.2 or 6.SP.A.2North Carolina - Standard Course of Study: 6.SP.2 |
|
Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape. |
|
Georgia Math and ELA Standards: 6.NR.2.3 |
|
Interpret numerical data to answer a statistical investigative question created. Describe the distribution of a quantitative (numerical) variable collected, including its center, variability, and overall shape. |
|
New York State Next Generation Learning Standards: 6.SP.2 |
|
Understand that a set of quantitative data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall shape. |
|
Tennessee Academic Standards: 6.SP.A.2 |
|
Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center (mean, median, mode), spread (range), and overall shape. |
|
Alabama Course of Study Standards: 23 |
|
Calculate, interpret, and compare measures of center (mean, median, mode) and variability (range and interquartile range) in real-world data sets. |
|
Arizona Academic Standards: 6.SP.A.3 |
|
Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation uses a single number to describe the spread of the data set. |
|
Common Core State Standards: Math.6.SP.3 or 6.SP.A.3Tennessee Academic Standards: 6.SP.A.3 |
|
Recognize that a measure of center for a numerical data set summarizes all of its values with a single number, while a measure of variation describes how its values vary with a single number. |
|
Georgia Math and ELA Standards: 6.NR.2.4 |
|
Design simple experiments and collect data. Use data gathered from realistic scenarios and simulations to determine quantitative measures of center (median and/or mean) and variability (interquartile range and range). Use these quantities to draw conclusions about the data, compare different numerical data sets, and make predictions |
|
North Carolina - Standard Course of Study: 6.SP.3 |
|
Understand that both a measure of center and a description of variability should be considered when describing a numerical data set.
|
|
New York State Next Generation Learning Standards: 6.SP.3 |
|
Recognize that a measure of center for a quantitative data set summarizes all of its values with a single number while a measure of variation describes how its values vary with a single number.Note: Measures of center are mean, median, and mode. The measure of variation is the range. |
|
Arizona Academic Standards: 6.SP.B.4 |
|
Display and interpret numerical data by creating plots on a number line including histograms, dot plots, and box plots. |
|
Common Core State Standards: Math.6.SP.4 or 6.SP.B.4 |
|
Display numerical data in plots on a number line, including dot plots, histograms, and box plots. |
|
Georgia Math and ELA Standards: 6.NR.2.5 |
|
Relate the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered. |
|
North Carolina - Standard Course of Study: 6.SP.4 |
|
Display numerical data in plots on a number line. |
|
New York State Next Generation Learning Standards: 6.SP.4 |
|
Display quantitative data in plots on a number line, including dot plots, and histograms. |
|
Ohio's Learning Standards: 6.SP.4 |
|
Display numerical data in plots on a number line, including dot plots (line plots), histograms, and box plots. (GAISE Model, step 3) |
|
Tennessee Academic Standards: 6.SP.B.4 |
|
Display a single set of numerical data using dot plots (line plots), box plots, pie charts and stem plots. |
|
Arizona Academic Standards: 6.SP.B.5aCommon Core State Standards: 6.SP.B.5.AKentucky Academic Standards (KAS): 6.SP.5.aMississippi College- and Career-Readiness Standards: 6.SP.5a |
|
Reporting the number of observations. |
|
Georgia Math and ELA Standards: 6.NR.2.6 |
|
Describe the impact that inserting or deleting a data point has on the mean and the median of a data set. Create data displays using a dot plot or box plot to examine this impact. |
|
North Carolina - Standard Course of Study: 6.SP.5.a |
|
Describe the collected data by: |
|
New York State Next Generation Learning Standards: 6.SP.5.a |
|
Report the number of observations. |
|
Arizona Academic Standards: 6.SP.B.5b |
|
Describing the nature of the attribute under investigation including how it was measured and its units of measurement. |
|
Common Core State Standards: 6.SP.B.5.BKentucky Academic Standards (KAS): 6.SP.5.bMississippi College- and Career-Readiness Standards: 6.SP.5b |
|
Describing the nature of the attribute under investigation, including how it was measured and its units of measurement. |
|
North Carolina - Standard Course of Study: 6.SP.5.b |
|
Analyze center and variability by: |
|
New York State Next Generation Learning Standards: 6.SP.5.b |
|
Describe the nature of the attribute under investigation, including how it was measured and its units of measurement. |
|
Alabama Course of Study Standards: 24 |
|
Represent numerical data graphically, using dot plots, line plots, histograms, stem and leaf plots, and box plots. |
|
Arizona Academic Standards: 6.SP.B.5cCommon Core State Standards: 6.SP.B.5.CKentucky Academic Standards (KAS): 6.SP.5.c |
|
Giving quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered. |
|
Georgia Math and ELA Standards: 6.NR.2.1 |
|
Describe and interpret the center of the distribution by the equal share value (mean). |
|
Massachusetts Curriculum Frameworks: 6.SP.B.5.c |
|
Giving quantitative measures of center (median, and/or mean) and variability (range and/or interquartile range), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered. |
|
Mississippi College- and Career-Readiness Standards: 6.SP.5c |
|
Giving quantitative measures of center (median and/or mean) and variability (interquartile range), as well as describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered. |
|
New York State Next Generation Learning Standards: 6.SP.5.c |
|
Calculate range and measures of center, as well as describe any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered. |
|
Ohio's Learning Standards: 6.SP.5.c |
|
Find the quantitative measures of center (median and/or mean) for a numerical data set and recognize that this value summarizes the data set with a single number. Interpret mean as an equal or fair share. Find measures of variability (range and interquartile range) as well as informally describe the shape and the presence of clusters, gaps, peaks, and outliers in a distribution. |
|
Tennessee Academic Standards: 6.SP.B.5.c |
|
Give quantitative measures of center (median and/or mean) and variability (range) as well as describing any overall pattern with reference to the context in which the data were gathered. |
|
Wisconsin Academic Standards: 6.SP.B.5.c |
|
Describing any overall pattern and any striking deviations from the overall pattern with reference to the context in which the data were gathered and the quantitative measures of center (median and/or mean) and variability (interquartile range and/or mean absolute deviation) were given. |
|
Arizona Academic Standards: 6.SP.B.5dCommon Core State Standards: 6.SP.B.5.DKentucky Academic Standards (KAS): 6.SP.5.dMississippi College- and Career-Readiness Standards: 6.SP.5d |
|
Relating the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered. |
|
Georgia Math and ELA Standards: 6.NR.2.2 |
|
Summarize categorical and quantitative (numerical) data sets in relation to the context: display the distributions of quantitative (numerical) data in plots on a number line, including dot plots, histograms, and box plots and display the distribution of categorical data using bar graphs. |
|
New York State Next Generation Learning Standards: 6.SP.5.d |
|
Relate the range and the choice of measures of center to the shape of the data distribution and the context in which the data were gathered. |
|
Ohio's Learning Standards: 6.SP.5.d |
|
Choose the measures of center and variability, based on the shape of the data distribution and the context in which the data were gathered. |
|
Tennessee Academic Standards: 6.SP.B.5.d |
|
Relate the choice of measures of center to the shape of the data distribution and the context in which the data were gathered. |
|
Pennsylvania Core Standards: CC.2.4.6.B.1 |
|
Demonstrate an understanding of statistical variability by displaying, analyzing, and summarizing distributions. |
|
Pennsylvania Core Standards: M06.D-S.1.1.1 |
|
Display numerical data in plots on a number line, including line plots, histograms, and box-and- whisker plots. |
|
Pennsylvania Core Standards: M06.D-S.1.1.2 |
|
Determine quantitative measures of center (e.g., median, mean, mode) and variability (e.g., range, interquartile range, mean absolute deviation). |
|
Pennsylvania Core Standards: M06.D-S.1.1.3 |
|
Describe any overall pattern and any deviations from the overall pattern with reference to the context in which the data were gathered |
|
Pennsylvania Core Standards: M06.D-S.1.1.4 |
|
Relate the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered. |
|
Georgia Math and ELA Standards: 6.NR.2.1 |
|
Describe and interpret the center of the distribution by the equal share value (mean). |
|
Georgia Math and ELA Standards: 6.NR.2.2 |
|
Summarize categorical and quantitative (numerical) data sets in relation to the context: display the distributions of quantitative (numerical) data in plots on a number line, including dot plots, histograms, and box plots and display the distribution of categorical data using bar graphs. |
|
Georgia Math and ELA Standards: 6.NR.2.3 |
|
Interpret numerical data to answer a statistical investigative question created. Describe the distribution of a quantitative (numerical) variable collected, including its center, variability, and overall shape. |
|
Georgia Math and ELA Standards: 6.NR.2.4 |
|
Design simple experiments and collect data. Use data gathered from realistic scenarios and simulations to determine quantitative measures of center (median and/or mean) and variability (interquartile range and range). Use these quantities to draw conclusions about the data, compare different numerical data sets, and make predictions. |
|
Georgia Math and ELA Standards: 6.NR.2.5 |
|
Relate the choice of measures of center and variability to the shape of the data distribution and the context in which the data were gathered. |
|
Georgia Math and ELA Standards: 6.NR.2.6 |
|
Describe the impact that inserting or deleting a data point has on the mean and the median of a data set. Create data displays using a dot plot or box plot to examine this impact. |
|
Arkansas Academic Standards: 6.SP.1 |
|
Identify the difference between statistical and non-statistical questions and write simple statistical questions that allow variable responses. |
|
Arkansas Academic Standards: 6.SP.2 |
|
Calculate and interpret any measure of center (mean, median, and mode) of a numerical data set. |
|
Arkansas Academic Standards: 6.SP.3 |
|
Determine which measure of center (mean or median) is more appropriate to describe the center of data and justify the choice. |
|
Arkansas Academic Standards: 6.SP.4 |
|
Describe how the mean or median is affected by outliers of a numerical data set. |
|
Arkansas Academic Standards: 6.SP.5 |
|
Calculate and interpret the measure of variation [range and interquartile range (IQR)] of a numerical data set. |
|
Arkansas Academic Standards: 6.SP.6 |
|
Determine which measure of variation (range or interquartile range) is more appropriate to describe the shape; justify the choice. |
|
Arkansas Academic Standards: 6.SP.7 |
|
Represent numerical data on a number line, histogram, and box plot. |
|
Arkansas Academic Standards: 6.SP.8 |
|
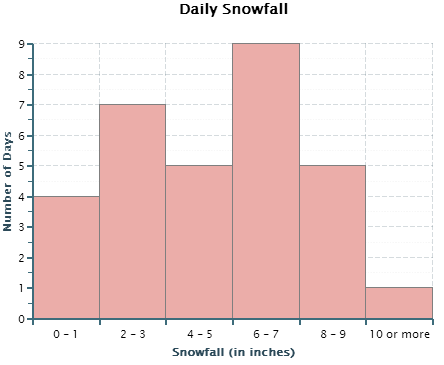
Calculate the relative frequency of an interval of data values when given a histogram. |
|
Arkansas Academic Standards: 6.SP.9 |
|
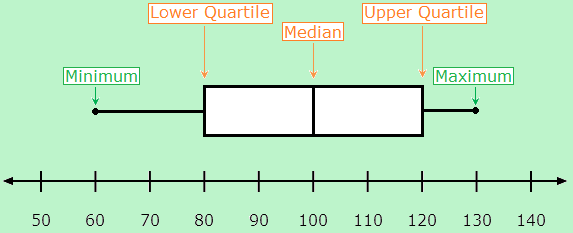
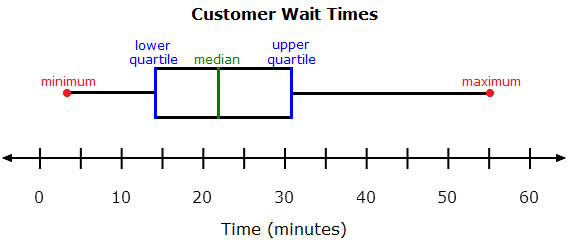
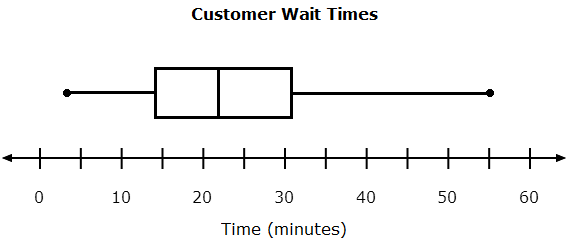
Interpret a box plot to answer statistical questions about a data set. |
|
 6th Grade Math - Data Displays & Analysis Lesson
6th Grade Math - Data Displays & Analysis Lesson