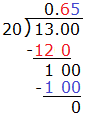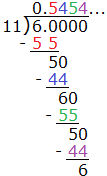Understanding Operations - Multiply/Divide
7th Grade
|
|
|
Alabama Course of Study Standards:
4.e
|
Extend strategies of multiplication to rational numbers to develop rules for multiplying signed numbers, showing that the properties of the operations are preserved. |
Arizona Academic Standards:
7.NS.A.2a
Common Core State Standards:
Math.7.NS.2a or 7.NS.A.2.A
Kentucky Academic Standards (KAS):
7.NS.2.a
Mississippi College- and Career-Readiness Standards:
7.NS.2a
|
Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (–1)(–1) = 1 and the rules for multiplying signed numbers. Interpret products of rational
numbers by describing real-world contexts. |
Georgia Math and ELA Standards:
7.NR.1.6
|
Make sense of multiplication of rational numbers using realistic applications. |
North Carolina - Standard Course of Study:
7.NS.2.a
|
Understand that a rational number is any number that can be written as a quotient of integers with a non-zero divisor. |
Alabama Course of Study Standards:
4.f
|
Divide integers and explain that division by zero is undefined. Interpret the quotient of integers (with a nonzero divisor) as a rational number. |
Arizona Academic Standards:
7.NS.A.2b
Common Core State Standards:
Math.7.NS.2b or 7.NS.A.2.B
Kentucky Academic Standards (KAS):
7.NS.2.a
Mississippi College- and Career-Readiness Standards:
7.NS.2b
|
Understand that integers can be divided, provided that the divisor is not zero, and every quotient of integers (with non-zero divisor) is a rational number. If p and q are integers, then –(p/q) = (–p)/q = p/(–q). Interpret quotients of rational numbers by describing real-world contexts. |
Georgia Math and ELA Standards:
7.NR.1.7
|
Show and explain that integers can be divided, assuming the divisor is not zero, and every quotient of integers is a rational number. |
North Carolina - Standard Course of Study:
7.NS.2.b
|
Apply properties of operations as strategies, including the standard algorithms, to multiply and divide rational numbers and describe the product and quotient in real-world contexts. |
Arizona Academic Standards:
7.NS.A.2c
Common Core State Standards:
Math.7.NS.2c or 7.NS.A.2.C
Kentucky Academic Standards (KAS):
7.NS.2.c
Mississippi College- and Career-Readiness Standards:
7.NS.2c
|
Apply properties of operations as strategies to multiply and divide rational numbers. |
Georgia Math and ELA Standards:
7.NR.1.9
|
Apply properties of operations as strategies to solve multiplication and division problems involving rational numbers represented in an applicable scenario. |
North Carolina - Standard Course of Study:
7.NS.2.c
|
Use division and previous understandings of fractions and decimals.- Convert a fraction to a decimal using long division.
- Understand that the decimal form of a rational number terminates in 0s or eventually repeats.
|
Alabama Course of Study Standards:
4.g
|
Convert a rational number to a decimal using long division, explaining that the decimal form of a rational
number terminates or eventually repeats. |
Arizona Academic Standards:
7.NS.A.2d
|
Convert a rational number to decimal form using long division; know that the decimal form of a rational number terminates in 0’s or eventually repeats. |
Common Core State Standards:
Math.7.NS.2d or 7.NS.A.2.D
Kentucky Academic Standards (KAS):
7.NS.2.d
Mississippi College- and Career-Readiness Standards:
7.NS.2d
|
Convert a rational number to a decimal using long division; know that the decimal form of a rational number terminates in 0s or eventually repeats. |
Georgia Math and ELA Standards:
7.NR.1.10
|
Convert rational numbers between forms to include fractions, decimal numbers and percentages, using understanding of the part divided by the whole. Know that the decimal form of a rational number terminates in 0s or eventually repeats. |
North Carolina - Standard Course of Study:
7.NS.2.d
|
Understand that the decimal form of a rational number terminates in 0s or eventually repeats. |
Pennsylvania Core Standards:
CC.2.1.7.E.1
|
Apply and extend previous understandings of operations with fractions to operations with rational numbers. |
Pennsylvania Core Standards:
M07.A-N.1.1.3
|
Apply properties of operations to multiply and divide rational numbers, including real-world contexts; demonstrate that the decimal form of a rational number terminates or eventually repeats. |
Georgia Math and ELA Standards:
7.NR.1.6
|
Make sense of multiplication of rational
numbers using realistic applications. |
Georgia Math and ELA Standards:
7.NR.1.7
|
Show and explain that integers can be
divided, assuming the divisor is not zero,
and every quotient of integers is a rational
number. |
Georgia Math and ELA Standards:
7.NR.1.8
|
Represent the multiplication and division of
integers using a variety of strategies and
interpret products and quotients of rational
numbers by describing them based on the
relevant situation. |
Georgia Math and ELA Standards:
7.NR.1.9
|
Apply properties of operations as strategies
to solve multiplication and division
problems involving rational numbers
represented in an applicable scenario. |
Arkansas Academic Standards:
7.NCC.4
|
Convert a rational number in fraction form to decimal form and recognize that the decimal form of a rational number terminates in 0s or eventually repeats. |
Arkansas Academic Standards:
7.NCC.5
|
Interpret the products and quotients of rational numbers by describing real-world contexts. |
Arkansas Academic Standards:
7.NCC.8
|
Use multiplication and division with rational numbers in any form to solve multi-step problems in real-world and mathematical contexts. |
Arkansas Academic Standards:
7.NCC.9
|
Apply operations with rational numbers involving the order of operations, involving nested grouping symbols. |
|
|


 7th Grade Math - Understanding Operations - Multiply/Divide Lesson
7th Grade Math - Understanding Operations - Multiply/Divide Lesson