Bivariate Data
8th Grade
|
|
|
Alabama Course of Study Standards:
18
|
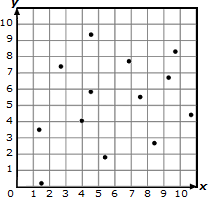
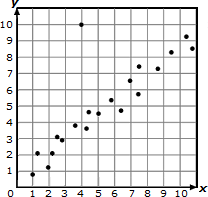
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between
two quantities, describing patterns in terms of positive, negative, or no association, linear and non-linear association,
clustering, and outliers. |
Arkansas Academic Standards:
8.SP.A.1
|
- Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities
- Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association
|
Arizona - K-12 Academic Standards:
8.SP.A.1
|
Construct and interpret scatter plots for bivariate measurement data to investigate and describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association. |
Common Core State Standards:
Math.8.SP.1 or 8.SP.A.1
Georgia Standards of Excellence (GSE):
MGSE8.SP.1
|
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association. |
North Carolina - Standard Course of Study:
8.SP.1
|
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Investigate and describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association. |
Ohio's Learning Standards:
8.SP.1
|
Construct and interpret scatter plots for bivariate
measurement data to investigate patterns of association between two
quantities. Describe patterns such as clustering; outliers; positive,
negative, or no association; and linear association and nonlinear
association. (GAISE Model, steps 3 and 4) |
Alabama Course of Study Standards:
19
|
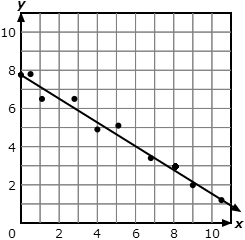
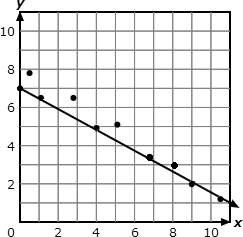
Given a scatter plot that suggests a linear association, informally draw a line to fit the data, and assess the model fit
by judging the closeness of the data points to the line. |
Arkansas Academic Standards:
8.SP.A.2
|
- Know that straight lines are widely used to model relationships between two quantitative variables
- For scatter plots that suggest a linear association, informally fit a straight line, and informally assess the model fit by judging the closeness of the data points to the line
For example: Identify weak, strong, or no correlation.
|
Common Core State Standards:
Math.8.SP.2 or 8.SP.A.2
Georgia Standards of Excellence (GSE):
MGSE8.SP.2
|
Know that straight lines are widely used to model relationships between two quantitative variables. For scatter plots that suggest a linear association, informally fit a straight line, and informally assess the model fit by judging the closeness of the data points to the line. |
North Carolina - Standard Course of Study:
8.SP.2
|
Model the relationship between bivariate quantitative data to:- Informally fit a straight line for a scatter plot that suggests a linear association.
- Informally assess the model fit by judging the closeness of the data points to the line.
|
New York State Next Generation Learning Standards:
8.SP.2
|
Understand that straight lines are widely used to model relationships between two quantitative variables. For scatter plots that suggest a linear association, informally fit a straight line, and informally assess the model fit by judging the closeness of the data points to the line. |
Ohio's Learning Standards:
8.SP.2
|
Understand that straight lines are widely used to model
relationships between two quantitative variables. For scatter plots that
suggest a linear association, informally fit a straight line, and
informally assess the model fit by judging the closeness of the data
points to the line. (GAISE Model, steps 3 and 4) |
Alabama Course of Study Standards:
20
|
Use a linear model of a real-world situation to solve problems and make predictions.- Describe the rate of change and y-intercept in the context of a problem using a linear model of a real-world
situation.
|
Arkansas Academic Standards:
8.SP.A.3
|
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercepts
For example: In a linear model for a biology experiment, interpret a slope of 1.5 cm/hr as meaning that an additional hour of sunlight each day is associated with an additional 1.5 cm in mature plant height. |
Arizona - K-12 Academic Standards:
8.SP.A.3
|
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept. |
Common Core State Standards:
Math.8.SP.3 or 8.SP.A.3
Georgia Standards of Excellence (GSE):
MGSE8.SP.3
|
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept. For example, in a linear model for a biology experiment, interpret a slope of 1.5 cm/hr as meaning that an additional hour of sunlight each day is associated with an additional 1.5 cm in mature plant height. |
North Carolina - Standard Course of Study:
8.SP.3
|
Use the equation of a linear model to solve problems in the context of bivariate quantitative data, interpreting the slope and y-intercept. |
New York State Next Generation Learning Standards:
8.SP.3
|
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept.
e.g., In a linear model for a biology experiment, interpret a slope of 1.5 cm/hr. as meaning that an additional hour of sunlight each day is associated with an additional 1.5 cm in mature plant height. |
Ohio's Learning Standards:
8.SP.3
|
Use the equation of a linear model to solve problems in the
context of bivariate measurement data, interpreting the slope and
intercept. For example, in a linear model for a biology experiment,
interpret a slope of 1.5 cm/hr as meaning that an additional hour of
sunlight each day is associated with an additional 1.5 cm in mature
plant height. (GAISE Model, steps 3 and 4) |
Wisconsin Academic Standards:
8.SP.A.3
|
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept.
For example, in a linear model for a biology experiment, interpret a slope of 1.5 cm/hr as meaning that an additional hour of sunlight each day is associated with an additional 1.5 cm in mature plant height. |
Alabama Course of Study Standards:
21
|
Construct and interpret a two-way table summarizing data on two categorical variables collected from the same
subjects, using relative frequencies calculated for rows or columns to describe possible associations between the two
variables. |
Arkansas Academic Standards:
8.SP.A.4
|
- Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table
- Construct and interpret a two-way table on two categorical variables collected from the same subjects
- Use relative frequencies calculated for rows or columns to describe possible association between the two variables
Example: Two-Way Frequency Table
Example: Two-Way Relative Frequency Table
For example: Students might be asked to interpret from the tables above, if they saw an SUV in the parking lot, would it be more likely to belong to a male or female?
Note: Suggested connections for instruction: Standard 8.NS.1. On the Two-Way Relative Frequency Table, it is not required to include the fractional representation for each value, this is simply provided as an example.
|
Arizona - K-12 Academic Standards:
8.SP.A.4
|
Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables. |
Common Core State Standards:
Math.8.SP.4 or 8.SP.A.4
|
Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables. For example, collect data from students in your class on whether or not they have a curfew on school nights and whether or not they have assigned chores at home. Is there evidence that those who have a curfew also tend to have chores? |
Georgia Standards of Excellence (GSE):
MGSE8.SP.4
|
Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table.
- Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects.
- Use relative frequencies calculated for rows or columns to describe possible association between the two variables. For example, collect data from students in your class on whether or not they have a curfew on school nights and whether or not they have assigned chores at home. Is there evidence that those who have a curfew also tend to have chores?
|
North Carolina - Standard Course of Study:
8.SP.4
|
Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table.- Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects.
- Use relative frequencies calculated for rows or columns to describe possible association between the two variables.
|
Tennessee Academic Standards:
8.SP.A.4
|
Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation. Understand that, just as with simple events, the probability of a compound event is the fraction of outcomes in the sample space for which the compound event occurs. Represent sample spaces for compound events using methods such as organized lists, tables, and tree diagrams. For an event
described in everyday language (e.g., "rolling double sixes"), identify the outcomes in the sample space which compose the event. |
Wisconsin Academic Standards:
8.SP.A.4
|
Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables.
For example, collect data from students in your class on whether or not they have a curfew on school nights and whether or not they have assigned chores at home. Is there evidence that those who have a curfew also tend to have chores? |
Pennsylvania Core Standards:
CC.2.4.8.B.1
|
Analyze and/or interpret bivariate data displayed in multiple representations. |
Pennsylvania Core Standards:
M08.D-S.1.1.1
|
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative correlation, linear association, and nonlinear association |
Pennsylvania Core Standards:
M08.D-S.1.1.2
|
For scatter plots that suggest a linear association, identify a line of best fit by judging the closeness of the data points to the line. |
Pennsylvania Core Standards:
M08.D-S.1.1.3
|
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept. |
Pennsylvania Core Standards:
CC.2.4.8.B.2
|
Understand that patterns of association can be seen in bivariate data utilizing frequencies. |
Pennsylvania Core Standards:
M08.D-S.1.2.1
|
Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible associations between the two variables. |
|
|
8th Grade Math - Bivariate Data Lesson
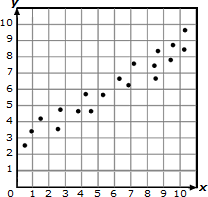
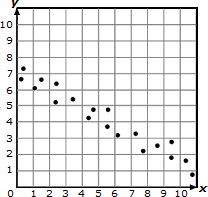
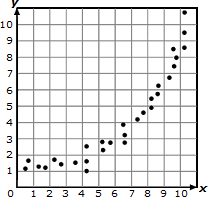nonlinear association
