A rational number can be written as a fraction ,
where and are integers and does not equal zero.
Integers, fractions, and repeating or terminating decimals are rational numbers.
Whole numbers are rational numbers greater than or
equal to zero that do not have a fraction or decimal {0, 1, 2, 3, ...}.
Integers are whole numbers and their opposites {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Natural numbers are rational numbers greater than
zero that do not have a fraction or decimal.
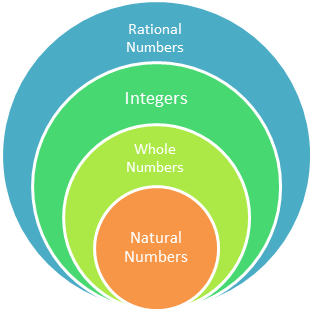
Natural numbers are a subset of whole numbers.
All natural numbers are whole numbers.
Some, but not all, whole numbers are natural numbers.
Whole numbers are a subset of integers.
All whole numbers are integers.
Some, but not all, integers are whole numbers.
Integers are a subset of rational numbers.
All integers are rational numbers.
Some, but not all, rational numbers are integers.


 7th Grade Math - Number Systems Lesson
7th Grade Math - Number Systems Lesson




