8.2.A 8.2.B

Real Numbers 8th Grade

Texas Essential Knowledge and Skills (TEKS): 8.2.A
extend previous knowledge of sets and subsets using a visual representation to describe relationships between sets of real numbers;
Texas Essential Knowledge and Skills (TEKS): 8.2.B
approximate the value of an irrational number, including ? and square roots of numbers less than 225, and locate that rational number approximation on a number line;

The set of real numbers can be divided into two subsets:
rational numbers and irrational numbers.

A rational number can be written as a fraction

\frac{p}{q}

,
where

p

and

q

are integers and

q

does not equal zero.

Integers, fractions, and repeating or terminating decimals are rational numbers.

An irrational number cannot be written as a fraction

\frac{p}{q}

,
where

p

and

q

are integers and

q

does not equal zero.

Non-repeating, non-terminating decimals are irrational numbers.

Whole numbers are rational numbers greater than or
equal to zero that do not have a fraction or decimal {0, 1, 2, 3, ...}.

Integers are whole numbers and their opposites {..., -3, -2, -1, 0, 1, 2, 3, ...}.

Natural numbers are rational numbers greater than
zero that do not have a fraction or decimal.

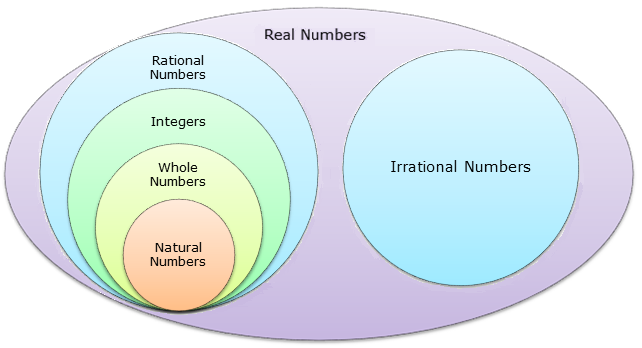
Rational numbers and irrational numbers are subsets of real numbers.

Integers are a subset of rational numbers, so integers are also real numbers.

Whole numbers are a subset of integers, so whole numbers are also rational numbers and real numbers.

Natural numbers are a subset of whole numbers, so natural numbers are also integers, rational numbers, and real numbers.

If a number is between two perfect squares, then the square root of
the number is between the square roots of the perfect squares.

Next, find the square roots of the perfect squares.

\begin{array}{rcl} \sqrt{25} & = & 5 \\ \sqrt{36} & = & 6 \end{array}

So,

\sqrt{30}

is between 5 and 6.

\sqrt{25} = 5

and

\sqrt{36} = 6

. 30 is about halfway between 25 and 36, so a better approximation of

\sqrt{30}

is probably between 5.4 and 5.6 because they are about halfway between 5 and 6.

30 is between 29.16 and 31.36, so a better approximation of

\sqrt{30}

is between 5.4 and 5.6.

Real Numbers

Texas Essential Knowledge and Skills (TEKS): 8.2.A

extend previous knowledge of sets and subsets using a visual representation to describe relationships between sets of real numbers;

Texas Essential Knowledge and Skills (TEKS): 8.2.B

approximate the value of an irrational number, including ? and square roots of numbers less than 225, and locate that rational number approximation on a number line;

Processing Request...