Dilations8th Grade |
|
|---|---|
Texas Essential Knowledge and Skills (TEKS): 8.3.A |
|
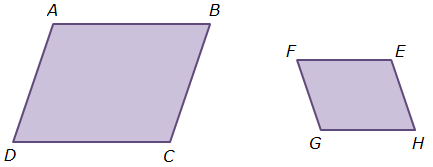
generalize that the ratio of corresponding sides of similar shapes are proportional, including a shape and its dilation; |
|
Texas Essential Knowledge and Skills (TEKS): 8.3.B |
|
compare and contrast the attributes of a shape and its dilation(s) on a coordinate plane; and |
|
Texas Essential Knowledge and Skills (TEKS): 8.3.C |
|
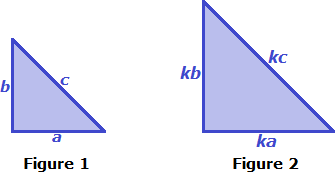
use an algebraic representation to explain the effect of a given positive rational scale factor applied to two-dimensional figures on a coordinate plane with the origin as the center of dilation. |
|
Texas Essential Knowledge and Skills (TEKS): 8.10.D |
|
model the effect on linear and area measurements of dilated two-dimensional shapes. |
|
Florida - Benchmarks for Excellent Student Thinking: MA.8.2.2 |
|
Given a preimage and image generated by a single dilation, identify the scale factor that describes the relationship. |
|
Florida - Benchmarks for Excellent Student Thinking: MA.8.2.4 |
|
Solve mathematical and real-world problems involving proportional relationships between similar triangles. |
|
 8th Grade Math - Dilations Lesson
8th Grade Math - Dilations Lesson