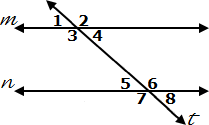
A transversal is a line which intersects two or more other lines.
In the image [above], lines m and n are cut by transversal t.
When lines intersect, a variety of angles are formed. Many of these angles have names.
In the image above, angles 3 and 6, and angles 4 and 5 are alternate interior angles.
When the lines cut by a transversal are parallel lines, alternate interior angles are congruent.
In the image above, angles 1 and 8, and angles 2 and 7 are alternate exterior angles.
When the lines cut by a transversal are parallel lines, alternate exterior angles are congruent.
In the image above, the following pairs of angles are corresponding angles: 1 and 5, 3 and 7, 2 and 6, and 4 and 8.
When the lines cut by a transversal are parallel lines, corresponding angles are congruent.
In the image above, angles 3 and 5, and angles 4 and 6 are same side interior angles.
When the lines cut by a transversal are parallel lines, same side interior angles are supplementary.
In the image above, the following pairs of angles are vertical angles: 1 and 4, 2 and 3, 5 and 8, and 6 and 7. Vertical angles are congruent.


 8th Grade Math - Angles & Triangles Lesson
8th Grade Math - Angles & Triangles Lesson