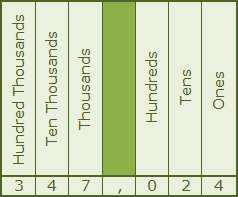
Common Core StandardsPlace Value |
|
|---|---|
| Grade: | 4th Grade |
| Standard: | CC.2.1.4.B.1 |
| Description: | Apply place-value concepts to show an understanding of multi-digit whole numbers. |
| Standard: | MA.4.NSO.1.1 |
| Description: | Express how the value of a digit in a multi-digit whole number changes if the digit moves one place to the left or right. |
| Standard: | MA.4.NSO.1.2 |
| Description: | Read and write multi-digit whole numbers from 0 to 1,000,000 using standard form, expanded form and word form. |
| Standard: | M04.A-T.1.1.1 |
| Description: | Demonstrate an understanding that in a multi-digit whole number (through 1,000,000), a digit in one place represents ten times what it represents in the place to its right. |
| Standard: | M04.A-T.1.1.2 |
| Description: | Read and write whole numbers in expanded, standard, and word form through 1,000,000. |
| Standard: | Math.4.NBT.1 or 4.NBT.A.1 |
| Description: | Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right. For example, recognize that 700 ÷ 70 = 10 by applying concepts of place value and division. |
| Standard: | Math.4.NBT.2 or 4.NBT.A.2 |
| Description: | Read and write multi-digit whole numbers using base-ten numerals, number names, and expanded form. Compare two multi-digit numbers based on meanings of the digits in each place, using >, =, and < symbols to record the results of comparisons. |
4th Grade Math - Place Value Lesson
