Start by finding the lengths of the sides of the rectangle.
Each square has a length of one unit.
Count the number of squares along each side of the rectangle to find its length.

Add the side lengths to find the perimeter.

So, the perimeter of the rectangle is 26 units.

Multiply the length and width to find the area.

So, the area of the rectangle is 36 square units.

The base of the triangle is 6 inches, and the height of the triangle is 8 inches.
Substitute the dimensions of the triangle into the formula to find the area.

Area	=	$\frac{1}{2}$× base × height
	=	$\frac{1}{2}$× 6 inches × 8 inches
	=	24 square inches

So, the area of the triangle is 24 square inches.

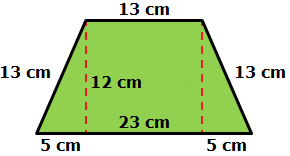
Start by decomposing the trapezoid into 2 congruent triangles and a rectangle.

Next, find the area of one of the triangles and the rectangle.

Area of Rectangle	=	length × width
	=	13 cm × 12 cm
	=	156 sq cm

Area of Triangle	=	$\frac{1}{2}$× base × height
	=	$\frac{1}{2}$× 5 cm × 12 cm
	=	30 sq cm

Then, find the sum of the 3 areas.

So, the area of the trapezoid is 216 square centimeters.

The net shows that the prism has two triangular faces with a base of 9 inches and a height of 8 inches and three rectangular faces with dimensions of 9 inches by 12 inches.

First, find the area of one of the triangular faces.

Area of Triangle	=	$\frac{1}{2}$× base × height
	=	$\frac{1}{2}$× 9 in. × 8 in.
	=	36 sq in.

Next, find the area of one of the rectangular faces.

Area of Rectangle	=	length × width
	=	12 in. × 9 in.
	=	108 sq in.

Then, add the areas of the faces.
Remember there are two triangular faces and three rectangular faces.

So, the surface area of the triangular prism is 396 square inches.