WORKING WITH ANGLE MEASURES
Vertical angles are the opposite angles formed by the intersection of two lines, line segments, and/or rays.
In the image [right], angles 1 and 4 are vertical angles, and angles 2 and 3 are vertical angles.
Vertical angles have the same measure. | 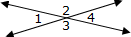 |
A linear pair is two adjacent angles which form a straight angle.
The sum of the two angle measures is 180°.
In the image [right], angles 1 and 2 form a linear pair. | 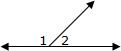 |
Supplementary angles are two angles whose measures sum to 180°.
Complementary angles are two angles whose measures sum to 90°.
Since triangle ABC is an equilateral triangle, angle 1 is 60°.
Angles 1 and 3 are vertical angles.
Vertical angles have the same measure.
So, the measure of angle 3 is 60°.
Angles 1 and 2 are adjacent angles which form a straight angle.
So, the sum of the measures of angles 1 and 2 is 180°.
Set up an equation and solve for the measure of angle 2.
| measure of angle 1 + measure of angle 2 | = | 180° |
| 60° + measure of angle 2 | = | 180° |
| measure of angle 2 | = | 180° - 60° |
| measure of angle 2 | = | 120° |
So, the measure of angle 2 is 120°.


 7th Grade Math - Angles Lesson
7th Grade Math - Angles Lesson





